大数の法則による統計的な力と条件付き大数の法則

#数楽 「大数の法則は統計的な力だ」という解釈の話の続き。コイン投げの例:表と裏に同じ割合でなるコイン投げをたくさん繰り返すと実際に出た表と裏の割合は1:1に近付きます。続く
#数楽 続き。その力をねじ曲げるために次のような魔法を使えるとしましょう。a>1/2とし、N回コインを投げて表の出た割合がa未満なら時間を巻き戻してやり直して表の割合がa以上になるまで繰り返す。この魔法を使われてしまうと、周囲の人達にはどのように見えるでしょうか?続く
#数楽 続き。任意のε>0に対して、Nを大きくすると、表の出た割合がa以上になるという条件の下での、表の割合がa+ε以上になる条件付き確率は0に近付きます。Nを大きくすると、まるで「表の割合を1/2に近付ける統計的な力」が働いているように見えるわけです。続く
#数楽 続き。表の割合を1/2に近付ける統計的な力が働いているところに、表の割合をa以上にする制限(魔法)をかけたので、結果的に表の割合がa以上からaに近付ける統計的な力が働いているように周囲の人たちには見えるわけです。以上の直観的に納得し易い話は大幅に拡張されます。続く
#数楽 コイン投げの確率分布q(表)=1/2、q(裏)=1/2と函数f(表)=1、f(裏)=0を考え、コインをN回投げて函数fの値の平均がa以上になる場合に制限するとき、続く
#数楽 続き。βはZ:=e^{-βf(表)}q(表)+e^{-βf(裏)}q(裏)、(1/Z)(e^{-βf(表)}q(表)f(表)+f(裏)e^{-βf(裏)}q(裏))=aで決めます。すなわちe^{-β}=a/(1-a)で、表:裏はa:(1-a)に近付く。続く
#数楽 続き。以上はコイン投げ+魔法の話を、一般の場合に通用する形で言い直したものになっています。もとの確率分布qと函数fは任意に取れるので大幅に適用可能な状況が広くなっています。続く
#数楽 続き。確率分布q=(q_1,…,q_r) (q_iは非負で総和が1)と任意確率変数f=(f_1,…,f_r)を取り、その平均をa_0=Σf_i q_iと書きます。確率分布qのN回の独立試行で出た1からrの目をi_ν (ν=1,…N)と書きましょう。続く
#数楽 続き。実数aを固定し、次の制限をかけます(魔法)。(1)a≧a_0のとき、(1/N)Σf_{i_ν}≧a(2)a≦a_0のとき、(1/N)Σf_{i_ν}≦a制限をかけないと(1/N)Σf_{i_ν}はfの期待値a_0に近付く大数の法則の力が働きます。続く
#数楽 続き。その力を妨げるように不等式で制限をかけるわけです。(例:指数分布の不平等に近付く力を妨げるためにlog型効用の総和に下限を設ける) その制限のもとでNを大きくすると、iの目の割合はp_i=e^{-βf_i}q_i/Z(β)に近付くことを示せます。ここで~続く
#数楽 続き~、Z(β)とβは以下で決めます:Σp_i=1 すなわち Z(β)=Σe^{-βf_i}q_i、Σf_i p_i=(1/Z)Σf_i e^{-βf_i}q_i=-(∂/∂β)log Z(β)=a.Z(β)の定義は割合の総和を1にするための条件です。続く
#数楽 実際に出た目に関するfの平均(1/N)Σf_{i_ν}が大数の法則によって期待値a_0に近付くことをaで妨げる条件を課したので、大数の法則の力によってNを大きくすると(1/N)Σf_{i_ν}はaに近付きます。それがΣf_i p_i=aという条件の意味です。続く
#数楽 続き。このように、割合(もしくは確率分布)の形が p_i=e^{-βf_i}q_i/Z(β) だとわかってしまえば、Z(β)とβを決める条件は直観的に当然そうなるべき条件なので、直観的に非自明なのは p_i が e^{-βf_i}q_i に比例することだけです。続く
#数楽 続き。確率変数fの経験平均が期待値に近付けないように不等式で制限をかけると、iの目の出る割合がq_iからそれにe^{-βf_i}をかけたものに比例するように変化するわけです。統計力学の用語を借りて、e^{-βf_i}をボルツマン因子と呼び、βを逆温度と呼びましょう。続く
#数楽 続き。というわけで、以上で述べたようなタイプの条件付き確率分布の極限を理解するためには、ボルツマン因子e^{-βf_i}がどのような仕組みで出てくるかを理解すればよいことになります。その辺の仕組みは本質的に統計力学の教科書に書いてあります。続く
#数楽 続き。統計力学の教科書では等確率の原理を仮定しており、確率と場合の数は定数倍を除いて同じものになります。そして場合の数の対数がある種の漸近挙動を満たすという仮定のもとでボルツマン因子を導出します。数学用語を使えばある種の大偏差原理を仮定するとボルツマン因子が出るという話。
#数楽 続き。統計力学では大偏差原理の成立が物理的な仮定になっているので、物理的とは限らないもっと一般の場合に統計力学の方法を適用するためには、必要な大偏差原理がいつ成立しているかを知る必要があり、数学的に様々な研究があります。詳しいことは確率論の専門家に聞いて下さい。続き
#数楽 続き。数学的にボルツマン因子がクリアに出て来る場合があることは、Sanovの定理について学べばわかります。有限集合上の確率分布のケースであれば非常に易しくて、難易度的には大学2年までにやる数学を知っていれば十分。詳しい解説→ http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20160616KullbackLeibler.pdf …
#数楽 続き。Sanovの定理からボルツマン因子が出て来ることの理解はほぼ相対エントロピー(大雑把には確率の対数)とその-1倍であるKullback-Leibler情報量の使い方の1つを学ぶことと同じになります。大した話でなくてかつ応用範囲は広いのにあんまり普及していない感じ。
#数楽 Kullback-Leibler情報量の定義はD(p|q)=Σp_i log(p_i/q_i)です。ここにlogが入っていることから、ボルツマン因子のexpが出て来る仕組みになっています。
#数楽 Kullback-Leibler情報量やボルツマン因子が出て来る仕組みを知りたければ、解説 http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20160616KullbackLeibler.pdf … を読んで下さい。易しい話から順番に説明してあるのでそこそこ読みやすいだろうと期待しています。
#数楽 Kullback-Leibler情報量に関するSanovの定理は、最尤法やベイズ統計や学習理論について学ぶときには必須の知識だと思う。その手の教養がないと、統計的モデルの予測精度の意味がわからなくなってしまいます。
#数楽 私の解説 http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20160616KullbackLeibler.pdf … を読めば逆温度βが負になっても気にならなくなるかも。統計力学における温度の概念の適用範囲は物理の外にある広大な数学の世界に広がっています。
#数楽 逆温度βについて。統計力学でのβは絶対温度Tのボルツマン定数k倍分の1です。β=1/(kT)。Tはtemperature(温度)の頭文字。a>1/2であるとし、コイン投げで表の出た割合をa以上に制限する場合には、e^{-β}=a/(1-a)>1となるのでβ<0となります。
#数楽 続き。逆温度にあたるものが負になるのは結構普通。統計力学で逆温度が負にならないのは、(熱浴と合わせた全体系のエネルギー保存則を仮定する前の段階では)注目する系のエネルギーに上界が無い場合を扱うのが普通でさらに等確率の原理を仮定しているから。
#数楽 制限を課す前の確率分布qに関する確率変数fの期待値をa_0=Σf_i q_iと書くとき、a_0より大きなaについて、大数の法則に妨げる制限を(1/N)Σf_{i_ν}≧aと設定すると、逆温度βは負になります。a_0=∞なら逆温度は負になりません。統計力学はそういう状況。
#数楽 Kullback-Leibler情報量に関するSanovの定理を仮定してボルツマン因子を出すことは易しい。(ボルツマン因子はもっと一般的な状況で出て来る。統計力学の教科書の方針に従えばよい。詳しくは http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20160616KullbackLeibler.pdf … の第7.2節を参照。)
#数楽 2つの確率分布p,qのKL情報量の定義はD(p||q)=Σ p_i log(p_i/q_i).確率q_iでiの目が出るルーレットを考える。そのルーレットをn回まわしたとき、iの目が出た回数をk_iと書くと、iの目が出た割合(経験分布)はp_i=k_i/n.続く
#数楽 続き。大雑把に言えば、Sanovの定理は(1/n)log(経験分布がp=(p_i)になる確率)=-D(p||q)+o(1)が成立することを意味します。o(1)はn→∞で0になる量です。KL情報量D(p||q)が少しでも大きくなるとn→∞で相対確率は0近付く。
#数楽 続き。すなわち大雑把にSanovの定理は「nが大きなとき、KL情報量D(p||q)は確率分布qによるn回の独立試行で経験分布pが実現する確率の対数の-1/n倍にほぼ等しい」ことを意味します。続く
#数楽 続き。さらに大雑把に言えば、「KL情報量D(p||q)は、確率分布qによる独立試行で偶然経験分布pが生じる確率が高いほど小さくなるように定められた確率分布qからpへの距離のようなものだ」と言うこともできます。KL情報量は確率モデルqによる真の分布pの予測の誤差の大きさ。
#数楽 Sanovの定理を認めれば、nが大きなとき、制限された確率分布qに従うn回の独立試行による経験分布k_i/nは制限の範囲内でKL情報量D(p||q)が最小になるp_iの近くに集中することがわかります。制限がΣf_i p_i≦aまたは≧aの既出のスタイルなら~続く
#数楽 続き~、KL情報量D(p||q)が最小になるp_iはL=D(p||q)+(λ-1)(Σp_i - 1)+β(Σf_i p_i-a)を用いたLagrangeの未定乗数法で得られます(未定乗数はλ-1とβ)。続く
#数楽 続き。∂L/∂λ=0はΣp_i=1を意味し、∂L/∂β=0はΣf_i p_i=aを意味する。∂L/∂p_i=0はlog(p_i/q_i)+λ+βf_i=0すなわちp_i=e^{-βf_i}q_i/Z,Z=e^λを意味します。ボルツマン因子が出て来た!
#数楽 続き。確率の総和が1になるという条件の未定乗数λ-1のλは分配函数の対数(Massieu函数)に等しく、制限Σf_i p_i≧aまたは≦aという制限に関する未定乗数βが逆温度(絶対温度分の1)になります。
#数楽 続き。このようにKL情報量の式の形を使えば、制限された範囲内でKL情報量が最小のpが経験的に実現されることからボルツマン因子が容易に出て来る。(実際にはもっと一般的な大偏差原理を仮定してもボルツマン因子が出て来る。KL情報量とSanovの定理のケースは制限し過ぎ。)
#数楽 というわけで、簡単な場合にボルツマン因子が出て来ることはKL情報量に関するSanovの定理に帰着できたわけです。残った仕事はSanovの定理の「証明」です。どこまでまじめに証明するかが問題になるのですが、応用が主体の人は以下の大雑把な理解で十分だと思います。続く
#数楽 まず、多項分布について学ぶ。次に、多項分布における確率(n!/(Πk_i!))Πq_i^{k_i}の対数をスターリングの公式を代入して近似計算する(p_i=k_i/nと置いておく)。その結果は-nD(p||q)+o(n)になる(Sanovの定理)。
#数楽 続き。階乗の近似式としてスターリングの公式は空気のごとく使われるので勉強の優先順位が高いです。早めに勉強してすっきりしておいた方がいいと思う。解説ノート http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20160616KullbackLeibler.pdf … の最初の方にスターリングの公式の導出も書いてあります。
#数楽 Lagrangeの未定乗数法もよく使われます(これも勉強するときの優先順位が高い)。多くの場合に決定された未定乗数は応用上重要な量になります。上の場合にλは分配函数の対数(Massieu函数)になり、βは逆温度(絶対温度分の1)になりました。
#数楽 Lagrangeの未定乗数法も直観的に明らかと思えるような理解の仕方があります。仕事の講義では証明の代わりに直観的な説明ですませているのですが、LaTeXで解説ノートを書いたことはない。
#数楽nは大きいとし、おもちゃのお金を十分たくさん用意して、n人にランダムに配る。「ランダムに配る」の数学的定義は「可能な場合はすべて等確率で生じる」という等確率の原理。このとき、n人に配られたおもちゃのお金の~続くhttps://twitter.com/i/moments/845895221728591872 …
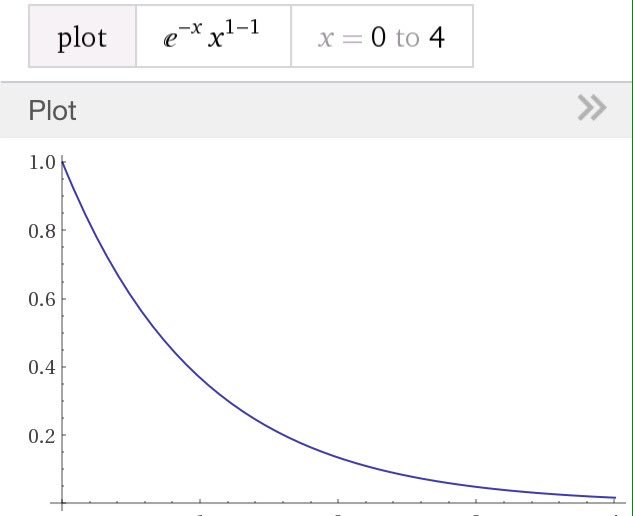
#数楽 続き~分布は指数分布で近似されるようになります。指数分布は添付画像のようなグラフになり、分布は0にピークがあります。続くpic.twitter.com/D9p1DJeerG
#数楽 続き。それだとあまりにも不平等な(おもちゃの)お金の配り方なので、i番目の人のお金をm_iと書き、log型効用の総和Σlog m_iに下限を設けることにしましょう(等確率の原理は保つ)。するとお金の分布はガンマ分布で近似されるようになります。続く
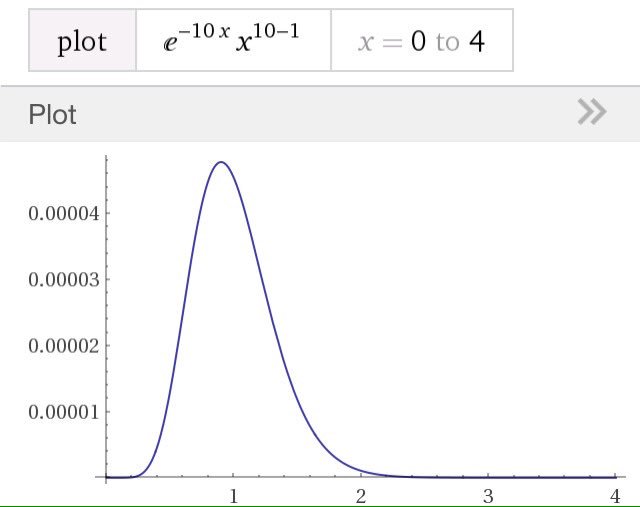
#数楽 続き。指数分布は平均のみをパラメーターに持ち、ガンマ分布ではパラメーターが二つに増えます。ガンマ分布は平均と分散で決まる。ガンマ分布のグラフの例は添付画像の通り。続くpic.twitter.com/xmiS7NisxX
#数楽 続き。単にランダムにお金を配るとお金の分布はピークが0でそこから指数函数的に単調現象する指数分布で近似される。しかし、log型効用の総和に下限を設けるとランダムに配られたお金の分布は平均の周囲が多数派のガンマ分布で近似されるようになる。以上は復習。続く
#数楽 続き。実際には、(log型)効用の総和の下限を低くし過ぎると、ランダムに配ったお金の分布は指数分布で近似されるままになってしまいます。指数分布ではないガンマ分布にするためには効用の下限は(平均)/e^γより大きくなければいけません。e^γ=1.781
#数楽 訂正「効用の下限」→「効用の平均の下限」。続き。そして、指数分布ではないガンマ分布になる場合にはlog型効用の総和は設けた下限にはりつくことになります。大数の法則的な統計的力は結構強力。要するにlog型効用の総和に設ける下限が低すぎると意味がないという話でした。
#数楽 訂正。イーカゲン過ぎた。式で書く。n人にnaペリカのおもちゃのお金を配るとき、log b_0=log a-γとb_0を定めると、b>b_0のとき、効用の総和の下限をΣlog m_i≧n log bとすると~続くhttps://twitter.com/genkuroki/status/847656152242339845 …
#数楽 続き~、ランダムに配ったお金の分布は指数分布ではないガンマ分布で近似されるようになる。要するにlog型効用の平均の下限をlog(平均)-γより大きくすれば指数分布ではないガンマ分布が出て来る。下限がそれ以下なら結果は指数分布のまま変わらない。γ=0.5772
#数楽 続き。配られるお金の一人当たりの平均がaのとき、配られたお金のlogの平均の最大値はlog aになります。(1/n)Σlog m_i≦log((1/n)Σm_i)=log a (相加相乗平均の不等式)。だから、配られたお金のlogの平均の可能な下限の最大値はlog a.
#数楽 続き。配られたお金の対数の平均(log型効用の平均)の下限を可能な最大値であるlog aよりもオイラー定数γ=0.5772…以上小さく取ると、ランダムにお金を配った結果は指数分布で近似されるままになってしまうわけです。オイラー定数が自然に出て来る面白い例になっている!
#数楽 オイラー定数γの定義は単調減少正値数列1+1/2+1/3+…+1/n-log nの極限。naペリカのお金をn人に配るとき、n等分して配る場合のlog型効用の平均はlog aで最大になり、log型効用の平均にlog a-γより大きな下限を設けるとガンマ分布になり、~続く
#数楽 続き~、下限をlog a-γ以下まで下げると分布は平均aの指数分布になる。この意味で「指数分布と等分配のデルタ分布の違いはちょうどオイラー定数γ=0.5772…の分だ」と考えることができます。1+1/2+1/3+…+1/Nとlog Nの差がこんな所に顔を出す。
#数楽 ガンマ函数の対数微分ψ(s)=Γ'(s)/Γ(s)(の-1倍)はオイラー定数γの一般化。ψ(1)=-γ、なぜならばψ(s)=lim_{n→∞}(log n-(1/s+1/(s+1)+…+1/(s+n))).
#数楽 現在 http://math.tohoku.ac.jp/~kuroki/LaTeX/ にアクセスできなくなっています。最近ずっと使いまわしている解説のコピーを以下の場所に置いておきました。http://genkuroki.web.fc2.com/20160501StirlingFormula.pdf …http://genkuroki.web.fc2.com/20160616KullbackLeibler.pdf …



